Lattices

Any calculation in Schwinger.jl will start with a Lattice. The only required parameter is the number of sites N. For any backend, N can be an even integer; for MPSKit, it can also be Inf. Other parameters can be specified as keyword arguments:

F: number of flavors (default 1)
periodic: whether the lattice is periodic (default false)
q: the integer charge of the fermions (default 1)
θ2π: the $\theta$-angle divided by $2\pi$ (default 0)
a: the lattice spacing in coupling units (default 1)
m: the physical mass (in coupling units); the mass shift is applied automatically. (default 0)
mlat: the mass parameter in the Hamiltonian (default -q^2 * F * a/8)
mprime: the coefficient of the hopping-type mass term (default 0)

The sites of the lattice are indexed from 1 to N. The electric field operators are laid out as in the diagram below.

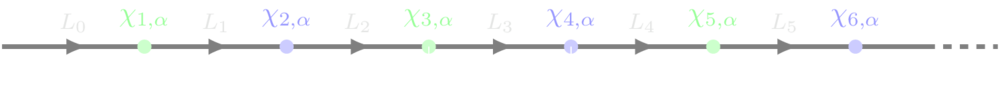
A Schwinger model lattice

Here $\alpha = 1,\ldots,F$ is a flavor index.

For details of how these parameters enter into the Hamiltonian, see here.

Schwinger.Lattice — Type

Lattice(;kwargs...)

Constructs a Lattice for the Schwinger model.

Arguments

N::Union{Integer,Inf}: Number of sites (use Inf for infinite lattices).
F::Int=1: Number of flavors.
periodic::Bool=false: Whether the lattice is periodic.
q::Int=1: Charge.
L::Union{Nothing,Real}=nothing: Length of the lattice.
a::Union{Nothing,Real}=nothing: Lattice spacing.
m::Union{Real,AbstractVector{<:Real},AbstractArray{<:Real,2}}=0.: Mass parameter.
mlat::Union{Nothing,Real,AbstractVector{<:Real},AbstractArray{<:Real,2}}=nothing: Lattice mass parameter.
mprime::Union{Real,AbstractVector{<:Real},AbstractArray{<:Real,2}}=0.: Hopping mass parameter.
θ2π::Union{Real,NTuple{N,Real}}=0.: Theta angle.

Returns

A Lattice object.

source